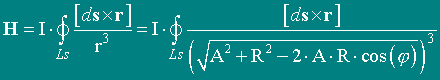The superficial current Is current on a hollow closed conductor between its poles A and B, it is possible to present as " strings of a current " i [Y.E.Tamm, Bases of the theory of an electricity, page 140], i.e. the currents which current on mathematical meridians of sphere from B to A.
It considerably simplifies the program of calculation of a magnetic field (MF) inside of the system of conductors equivalent on electromagnetic properties (in necessary approach) to spherical Closed and Hollow Conductor (CHC).
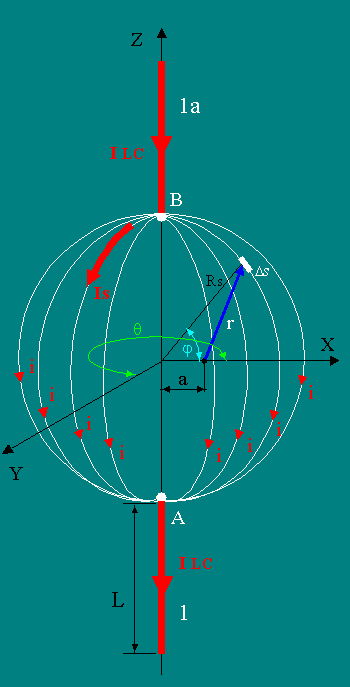
The Biot-Savart-Laplas law.
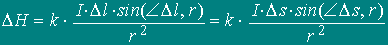
Or in the vector form 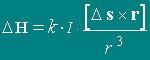
|
Radius of approximated CHC |
Rs = 1 | |
|
Quantity of strings of a current |
NL = 400 |
n = 0.. NL - 1 |
|
An angular step between strings |
Δ q = 2 × p / NL | |
|
Quantity of elements of a current |
NΔl = 200 |
m = 0.. NΔl - 1 |
|
An angular step centre to centre elements |
Δ j = p / NΔl |
|
Number of points of supervision |
Na = 100 |
a = 0.. Na - 1 |
|
Coordinate of "X" points of supervision |
s(a) = a×( R / Na ) |
|
A superficial current |
Is = 1 |
|
|
A current in a string |
i = Is / NL |
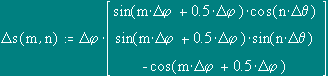
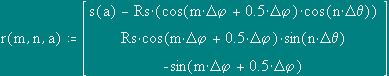
Because of axial symmetry of system pays off only tangential, q-component of MF.
In a considered case it is an Y-component, that is designated in Mathcad, as an index ( 1) at vector product.
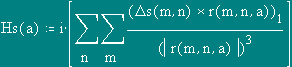
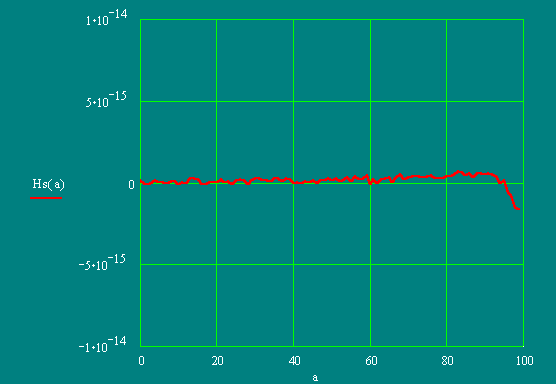
Accuracy of approximation of CHC can be increased by more quantity of strings of a current.
NL = 1000; NΔl = 1000
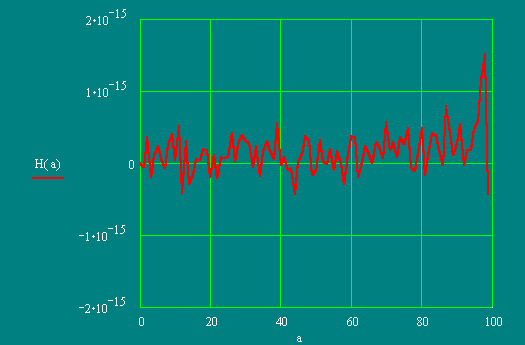
NL = 2000; NΔl = 2000
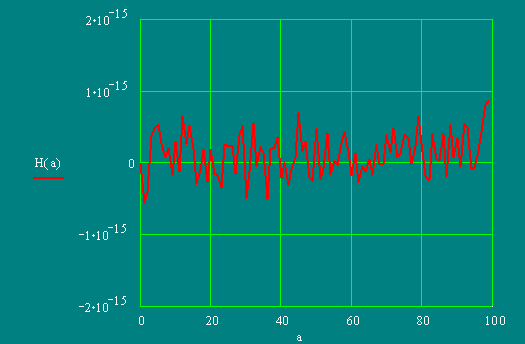
NL = 5000; NΔl = 5000
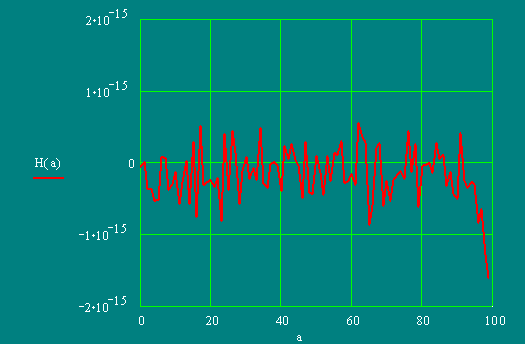
In this case, accuracy of the account is sufficient to believe result authentic.
Check by BASIC confirms calculation. File sphere.bas
In practice as more as possible exact approximation of electromagnetic properties of CHC on distance (0 ÷ 0.85) R from the center is interesting.
On the schedule it is visible, that the initial data satisfy to this condition.
Calculation of a magnetic field from bringing conductors 1 and 1a along axis . Is = I LC
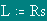
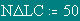 Number of elements of splitting of a bringing conductor
z:= 0..NDL - 1
Number of elements of splitting of a bringing conductor
z:= 0..NDL - 1
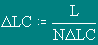
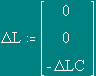
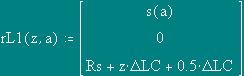
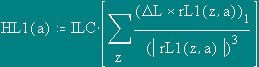
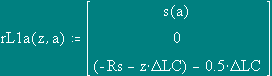
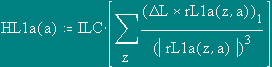

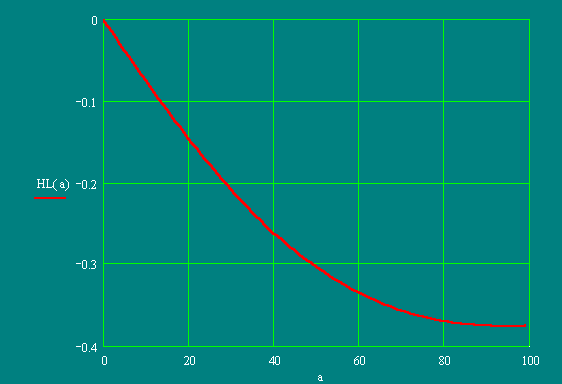
Comparing with results of two calculations it is possible to draw following conclusions:
1. The Magnetic field inside CHC is defined only by a current of bringing conductors (a difference in values of intensity - 14 orders);
2. Within the limits of accuracy of the machine account, the magnetic field created inside CHC by a current, current on its surface and between its poles, is equal to zero.
 File Mathcad in Zip-archive: sfera.zip
File Mathcad in Zip-archive: sfera.zip
Qbasic, unpack and work, see sphere.bas
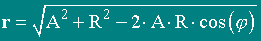 The module of a radius-vector from an element of a current in a point of supervision
The module of a radius-vector from an element of a current in a point of supervision