© Евгений Александрович Григорьев
Дополнение к IV уравнению Максвелла
и закону Ампера (полного тока).
Логика, расчет, эксперимент.
Показана недостаточность закона полного тока в электрических цепях,
включающих в себя полый замкнутый проводник.
Известно, что закон Ампера, под которым мировая наука понимает закон полного тока, появился как результат большого числа тщательных экспериментов с различными конфигурациями электрических цепей постоянного тока. Эти эксперименты объединяло одно - все цепи были линейными - только в них контур, по которому рассчитывается циркуляция вектора напряженности магнитного поля либо охватывает проводник, либо нет. То, что Ампер работал с линейными цепями, отмечает Наталия Ткаченко в своей обзорной работе "История электромагнетизма". В то время, когда формулировался закон полного тока (закон Ампера), отсутствовала возможность численного расчета магнитного поля внутри полого замкнутого проводника (ПЗП), поля, создаваемого текущим по поверхности ПЗП и между его полюсами током. Аналитическое выражение такого векторного поля содержит эллиптический интеграл второго рода и, поэтому, не может быть приведено к элементарному виду для простых численных расчетов. Теоретики, со вполне обоснованной осторожностью, рассматривали только линейные контуры с током. Д.К. Максвелл, занимавшийся разработкой теории переменных полей, принял закон Ампера, как очевидную аксиому и только дополнил его уравнение током смещения. Хотя, как утверждает
Г.В.Николаев в работе "Кризис в фундаментальной физике. Есть ли выход!?" сам Максвелл отмечал, что полученная им система уравнений не является полной и что она неприменима, например, для случая незамкнутых токов, отрезков тока и отдельных элементов тока.
Начнем с азов и очевидного.
Невозможно создать отдельный, незамкнутый отрезок проводника, в котором течет постоянный ток (незамкнутый элемент постоянного тока) - это нарушает закон сохранения заряда (Рис.1).
Поэтому кажется очевидным, что невозможно создать постоянное магнитное поле (МП) посредством отдельного элемента постоянного тока [1, с.163]. Логика этого вывода проста - нет объекта для рассмотрения. Таким образом, приравниваются понятия “отдельный, незамкнутый элемент постоянного тока” и “отдельный элемент постоянного тока” - часть замкнутой электрической цепи. На основании этой логики интерпретируются известные экспериментальные факты и сделаны выводы в теории электромагнетизма.
1) Проводник - тело, в котором есть движение зарядов, т.е. электрический ток, если внутри проводника напряженность электрического поля Е отлична от нуля. [1, с.26]. 2) Закон обратных квадратов. Это закон о центральных полях создаваемых центрами сил (гравитационные массы, электрические заряды, магнитные полюсы) по закону обратной пропорциональности квадрату расстояния. Говорится об одинаковом описании таких полей [1, с.19], [1, с.46]. Известно, что тело, находящееся внутри гравитирующей полой сферы, силы тяготения не испытывает.
3) В пространстве, окружающем произвольный ток, всегда есть МП [1, с.161].
4) Замкнутый проводник (ЗП) - тело, обеспечивающее протекание тока по замкнутому линейному контуру [1, с.164, с.167]. Обычно этот контур неразветвленный. Контур выполнен из линейного, металлического проводника. Ток, текущий по ЗП, создает МП во всем окружающем пространстве (см. п.3).
5) "...мы в основу всех наших рассуждений положим определенный закон, определяющий магнитное поле элемента тока, рассматривая этот закон как данный опытом.
I - сила тока в проводнике; ds - элемент линейного проводника; R - расстояние от элемента тока
Ids, создающего МП, до точки, где наблюдается напряженность H этого МП.
6) Полый замкнутый проводник (ПЗП) - проводящее тело в виде неразрывной замкнутой поверхности, которая полностью охватывает некоторый объем [2, с.65]. Обычно, это поверхность тела вращения - цилиндрическая или сферическая. Точки пересечения поверхности и оси симметрии - полюса. Ток, текущий по ПЗП между полюсами, не создает МП в объеме, который он обтекает, а более точно - векторная сумма магнитных полей, создаваемых всеми элементами этого тока, в любой точке внутри ПЗП равна нулю [ полная компенсация, вытекающяя из принципа суперпозиции ].
Это свойство ПЗП вытекает из законов Био-Савара-Лапласа и “обратных квадратов” (см. п.2, п.5). Иначе следует предположить, что напряженность МП, возбуждаемого элементом тока, изменяется по закону отличному от закона обратной пропорциональности квадрату расстояния, а это противоречит опыту. Это же свойство ПЗП подтверждается численными расчетами (аналитика упирается в эллиптический интеграл второго рода).
Минимальное количество участков обоих типов, нужных для создания замкнутой электрической цепи - два (Рис. 2, Рис. 3).
На рисунках обозначены: 1 - сферический ПЗП (сечение); 2- линейный проводник; I - ток, текущий в цепи; W - объем, охватываемый ПЗП.
Проанализируем цепь, показанную на Рис. 2.
Обозначим полюса ПЗП как А и В (Рис. 4).
Линейный проводник 2, представим в виде полубесконечных прямолинейных отрезков -¥А и +¥В, лежащих на одной оси. Созданная цепь с током имеет осевую симметрию. При этом, силовые линии МП имеют исключительно азимутальную (тангенциальную) компоненту. Они являются окружностями с центром на оси системы. Рассмотрим точку P. Она принадлежит контуру L. Контур L находится в объеме W и совпадает с предполагаемой, пока, силовой линией. ПЗП охватывает объем W.
Найдем циркуляцию вектора напряженности МП по контуру L. По определению: “Если кривая L замкнута, что отмечается кружком у знака интеграла, то линейный интеграл вектора а вдоль нее называется циркуляцией а вдоль L [1, с.469] ”:
В дальнейшем, элемент контура L будем обозначать dl, а элемент цепи Ls - ds.
Так как в нашем случае вектор H всегда параллелен dl, то:
Согласно принципу суперпозиции для цепи с током: “... напряженность поля H замкнутого тока I в произвольной точке P равна сумме полей, возбуждаемых каждым из его элементов, т.е. равна [1, с. 164] ”:
В этом выражении подразумевается, что ток течет по линейному замкнутому контуру, по которому происходит интегрирование. Тем не менее, оно применимо к любой токовой системе.
В случае бесконечного прямолинейного проводника, совпадающего с осью рассматриваемой системы (Рис. 4а), все его элементы давали бы вклад в МП в точке P (R - радиус-векторы от элементов тока в точку наблюдения P).
Однако, в рассматриваемом случае, ток, который течет по ПЗП 1, не создает МП в объеме W (см. п.6) и формула (42.4) будет выглядеть так:
а циркуляция вектора напряженности магнитного поля по замкнутой кривой L
Очевидно, что в рассматриваемой цепи циркуляция вектора напряженности магнитного поля по замкнутой кривой L, не охватывающей токов, не равна нулю, а предполагаемая силовая линия оказалась реальной. Это противоречит теореме о циркуляции вектора напряженности МП, в которой говорится о том, что: “...циркуляция вектора напряженности магнитного поля по кривой, не охватывающей токов, равна нулю... ” [1, с.178].
Откуда это противоречие? Попробуем разобраться.
Теорема Стокса .
“Циркуляция произвольного вектора а по замкнутой кривой L равна потоку ротора этого вектора через поверхность S, опирающуюся на кривую L ” [1, с.472]:
Давно была выведена и без обсуждения применяется формула [1, с.177]:
Теорема Стокса – чисто математическая, в ней нет ни слова о потоке зарядов через поверхность S – зарядов, создающих поток ротора. Тем не менее, утверждается: “На основании теоремы Стокса и уравнения (47.3) мы можем записать [1. с.177] ” :
Очевидно, что происходит прямая подмена ротора вектора на ток, т. е. на вектор, который образует этот самый ротор. Это - следствие той самой, “очевидной” логики рассуждений. Можно сделать вывод, что уравнение (47.3), в данном случае, не работает и требует теоретической доработки, а “...полная система дифференциальных уравнений магнитного поля постоянных токов...” [1. с.182] не является полной, как и система уравнений Максвелла - СОВСЕМ НЕ ОЧЕВИДНО И НЕ ОБЯЗАТЕЛЬНО СОБЛЮДЕНИЕ РАВЕНСТВА :
Так произошло потому, что электрическим током, в том числе и постоянным, называется упорядоченное движение носителей заряда. При таком движении за конечное время через некоторую площадку переносится отличный от нуля электрический заряд. Движущиеся упорядочено носители заряда определенного знака называются носителями тока и именно они ответственны за создание магнитного поля.
Тем не менее, постепенно, закон Ампера, в его изначальной формулировке, был принят, как норма, а теорема о циркуляции вектора напряженности МП стала, со временем, научной догмой. Из-за безоговорочного авторитета основоположников электромагнетизма и электродинамики и их, не менее знаменитых последователей и толкователей, другие токовые системы в дальнейшем не просчитывались, что значительно затормозило развитие теории и вытекающих из нее прикладных знаний. Наступило время заполнить этот пробел в электродинамике.

Рис.1
Проверим полноту этой логики.
Будем рассматривать только электрические цепи постоянного тока, в частности, отдельные части этих цепей, являющиеся суммой составляющих их элементов тока.
Именно так был выведен закон Био-Савара-Лапласа.
Терминология:

Линейный проводник и область создаваемого им МП.
[ Интересна постановка опыта, если на той же странице, выше, утверждается, что невозможно создать постоянное магнитное поле посредством отдельного элемента постоянного тока.
Стало быть, расчет, но как? Электрон, еще, не открыт (1897 г.), квантовая механика ( 1900 г. ) появится еще позднее. Е. Г. ]
Закон этот носит название закона Био-Савара
[ 1820 г. ] и в векторной форме может быть записан так " [1, с. 163]:


Полый замкнутый проводник и область создаваемого им МП.
Итак, в замкнутой электрической цепи с током могут существовать проводящие участки двух типов:
1) создающие МП всюду; 2) создающие МП всюду за исключением некоторого объема, который они охватывают.

Замкнутая электрическая цепь из двух типов проводников и область создаваемого ею МП.

Рис. 2

Рис. 3

Рис. 4

Рис. 4a
 (23*)
(23*)

 (42.4)
(42.4)



 (47.3)
(47.3)
 (47.4)
(47.4)

Постоянное магнитное поле является случайной, статистической суперпозицией полей элементарных движущихся носителей заряда, создающих постоянный электрический ток.
Поэтому, рассматривая любую систему постоянных токов, применительно к создаваемому ими магнитному полю, необходимо применять принцип суперпозиции и закон Био-Савара-Лапласа к каждому движущемуся носителю заряда - источнику переменного электрического поля .
Тогда в уравнении (47.3), полная форма которого

Повторно можно отметить, что так произошло потому, что раньше, когда формулировался закон полного тока, отсутствовала возможность численного расчета магнитного поля внутри ПЗП, создаваемого всеми движущимися по поверхности ПЗП и между его полюсами носителями зарядов. Аналитическое выражение такого векторного поля содержит эллиптический интеграл второго рода и, поэтому, не может быть приведено к элементарному виду для простых численных расчетов. Теоретики, со вполне обоснованной осторожностью, рассматривали только линейные контуры с током. Постепенно, это вошло в норму, а теорема о циркуляции вектора напряженности МП стала, со временем, научной догмой. Из-за этого другие токовые системы в дальнейшем не просчитывались, что значительно затормозило развитие теории и вытекающих из нее прикладных знаний.
Кратко повторим логику вывода.
Или есть два типа проводников с постоянным током (1 - создающие МП во всем окружающем пространстве; 2 - создающие МП во всем окружающем пространстве за исключением части пространства, которую они охватывают;) – или неверны законы Био-Савара-Лапласа и обратных квадратов.
2) Или есть замкнутые цепи постоянного тока, где циркуляция вектора напряженности магнитного поля по замкнутой кривой L, не охватывающей токов, не равна нулю – или неверен принцип суперпозиции.
Рассмотрим последствия этих рассуждений.
Во-первых, нужно исключить бесконечность из формул и создать реальную физическую систему.
Создадим осесимметричную замкнутую цепь (Рис.5), состоящую из двух линейных проводников AC, BD и двух сферических ПЗП 1 и 2, вложенных один в другой и не касающихся друг друга. Линейный проводник BD соединяет верхние полюса ПЗП 1 и 2. Линейный проводник AС соединяет нижние полюса ПЗП 1 и 2. Стрелками показано направление токов в цепи.
На Рис. 5а показан возможный вариант подвода питания к цепи.

Рис. 5 |

Рис. 5a |
Теперь формула (42.4) будет выглядеть так:

а циркуляция вектора напряженности МП по контуру L будет:

так как ПЗП 1 и 2 не создают МП в объеме W (см. п.6). Очевидно, что МП в объеме W есть сумма МП отдельных отрезков цепи - AC и BD.
Рассчитанная численным методом структура магнитного поля в плоскости Y = 0 (XZ) в виде графика Кантора показана на Рис. 6.

Показаны сечения поверхностей уровня равной напряженности МП.
Вектор напряженности направлен перпендикулярно плоскости рисунка.
Рис. 6
Такое МП имеет следующие особенности :
1) линию нулевой напряженности поля (ЛНН);
2) минимум напряженности в центре системы (исключая ЛНН);
3) градиент такой, что напряженность поля возрастает по направлению из центра кривизны силовых линий.
Таким образом, для исследования и применения введен новый класс постоянных магнитных полей - полей создаваемых отдельными элементами электрической цепи постоянного тока.
В природе такое МП существует в любом токовом канале, где ток обходит какое то препятствие. В таком канале с током I (Рис. 7) всегда можно найти трубку тока i (вплоть до отдельной движущейся заряженной частицы - ДЗЧ), диаметр d которой меньше размера неоднородности D. В частности, так может возникать в канале линейной молнии шаровая молния [ШМ].

Рис. 7
Такое МП существует в пространстве между двумя ДЗЧ, движущимися по одной линии и в одну сторону (Рис.8).

Рис. 8
Некоторые из эквипотенциальных поверхностей (сечения).
Вектор напряженности МП направлен перпендикулярно плоскости рисунка.
Конфигурация МП (Рис.9) подобна полю в “пробкотроне” [3], но с зеркальным отношением более 100 и исключительно азимутальной (тангенциальной) компонентой силовых линий. Из-за явного сходства, такое МП названо “магнитный кокон”. Конфигурация МП в “магнитном коконе” соответствует условию минимума напряженности поля [4]. Это позволяет создать давно ожидаемую ловушку для плазмы и термоядерный реактор с непрерывным магнитным удержанием плазмы [5]. Такое МП найдено экспериментально у тороидальных токовых структур (см. далее).

Рис. 9
Показаны некоторые из силовых линий одной из эквипотенциальных поверхностей.
Сечения поверхностей изображены на Рис.8.
Представляет интерес исследование поведения свободных радикалов в переменном МП такой конфигурации. Расчеты показывают, что должны образовываться спиральные полимерные структуры подобные ДНК.
Согласно расчетам, плазменные ДЗЧ в “магнитном коконе” создадут тороидальное образование с полоидальным вектором скорости частиц и R → r - каустикой (Рис.10). Такие, примерно, плазменные тороидальные структуры наблюдались и измерены в экспериментах по лазерному УТС ( 1, 2 )

Рис. 10
При нарастании МП, ларморовский радиус ДЗЧ будет уменьшаться – плазма будет всесторонне обжиматься. Эффект назван “сферический пинч”. В тороидальном образовании концентрация зарядов в тороидальном слое будет намного выше, чем в металлах. Это повысит коэффициент преломления гамма-лучей - возможно создание эффективной гамма-оптики.
В каустике будут происходить столкновения частиц и протекать реакции ядерного синтеза водородного, углеродного и других циклов. Тороидальное образование может изменять размер под влиянием внешних сил. МП в системе изменится - можно создать детектор этих сил.
Если ДЗЧ влетает под углом в МП такой конфигурации, то она будет отражаться от “магнитных стенок” (Рис. 11).

Рис. 11
Это эквивалентно системе МП в ондуляторах - системах, используемых в релятивистской электронике для создания генераторов излучения (лазер на свободных электронах).
Такую же конфигурацию имеет переменное МП в зазоре ненагруженного антенного диполя ( —— —— ), при наведениии в нем ЭДС сторонним переменным электромагнитным полем.
На основе МП такой конфигурации сейчас создаются устройства,
являющиеся, по сути, разными режимами работы двух соосных торов:
РЕГУЛИРУЕМЫЙ ОНДУЛЯТОР относится к ускорительной технике и может использоваться для создания генератора излучения, регулируемого в широком (СВЧ - VISUAL) диапазоне частот и выходной мощности.
УСТРОЙСТВО ДЛЯ УДЕРЖАНИЯ ПЛАЗМЫ относится к технике плазмы. Может быть использовано для создания плазменных установок, реактивных двигателей нового поколения и автономных, экологически чистых, безопасных источников энергии от 1 до 50 кВт.
В результате серии экспериментов выявилась, совершенно не очевидная изначально, трансформация устройства, показанного на Рис.5, в два соосных тора, как это показано на Рис. 12. Свойства этих тороидальных структур были рассмотрены теоретически и математически смоделированы. Конфигурация их магнитного поля измерена экспериментально.

Рис. 12
Трансформация устройства, показанного на Рис.5, в два соосных тора.
Тонкими линиями показаны сечения ПЗП: сферических (a), цилиндрических (b,c,d).
Толстыми линиями показаны линейные проводники, соединяющие полюса ПЗП.
На Рис.12с видно, что токи, текущие по внешнему и внутреннему цилиндрическим ПЗП на участке 1-2 полностью, с любой, необходимой степенью точности компенсируют друг друга в плане создания МП.
Поэтому, эти участки могут быть исключены из цепи, а сама цепь может быть заменена двумя торами, которые эквивалентны исходной цепи по созданию МП типа "магнитный кокон" в центре системы.
Теперь рассмотрим электрическую цепь, показанную на Рис. 3.
Теорема о циркуляции вектора напряженности магнитного поля (МП) гласит: “...циркуляция вектора напряженности магнитного поля по кривой,... охватывающей токи, равна помноженной на 4p/с сумме сил этих токов (взятых с надлежащими знаками).” [1, с.178]. Из теоремы следует, что циркуляция постоянна и не зависит от геометрии цепи.
Проверим положение теоремы.
Создадим осесимметричную замкнутую цепь (Рис.13), состоящую из сферического ПЗП 1 и линейного проводника 2. Линейный проводник соединяет полюса ПЗП. Стрелками показано направление токов в цепи.

Рис. 13
Из-за симметрии силовые линии МП имеют только азимутальную составляющую. Они являются окружностями с центром на оси системы. Рассмотрим точку P, принадлежащую контуру L. Контур L совпадает с силовой линией. Найдем циркуляцию вектора напряженности МП по контуру L. Циркуляция вектора H вдоль замкнутой кривой L определяется выражением
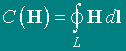
Так как в нашем случае H параллелен dl, то

Чтобы убедиться в справедливости теоремы, необходимо и достаточно доказать, что напряженность МП в точке P постоянна при изменении размеров системы (контур интегрирования L и ток I в линейном проводнике постоянны). ПЗП 1 не создает МП в объеме, который он охватывает (см. п.6). Поэтому, согласно принципу суперпозиции, можно рассматривать только линейный проводник 2. Обозначим проводник 2, как АВ (Рис. 14).

Рис. 14
По тому же принципу, напряженность МП Н тока I в произвольной точке P равна сумме полей его элементов :

I - сила тока в проводнике; ds - элемент цепи; Ids - элемент тока; R - расстояние от элемента тока до точки Р.
Отметим, что линейный проводник, создающий МП, имеет конечный размер.
Увеличим размеры системы (Рис. 15).

Рис. 15
ПЗП 1 все так же не создает МП в объеме, который он охватывает (см. п.6), а напряженность МП в точке Р из-за дополнительных вкладов отрезков тока AC и BD увеличится и станет:

Очевидно, что напряженность МП в точке Р изменяется при изменении размеров системы, что противоречит положению теоремы. Это и нужно было показать.
Цепь, показанная на Рис. 3, также, может быть трансформирована в тор.

Трансформация замкнутой цепи из двух типов проводников в тор и область МП, создаваемого ею (классическое представление - все МП сосредоточено внутри тора).
Видно, что линейный проводник имеет конечный размер и преобразуется в элемент тока.
Эквивалентность МП, создаваемого током,
текущим по линейному и полому цилиндрическому проводникам.

Рис. 16 |
 Рис. 17 |
Очевидно, что напряженность МП в точках 1 будет H º 0. Затем, по мере приближения к точке 2, Н будет нарастать, а после прохождения максимума (точка 3), чье расположение зависит от геометрии цепи - уменьшаться по закону, отличному от 1/R и 1/R2.

Рис. 18 |
 Рис. 19 |
Теперь, на основании показанной эквивалентности, трансформацию цепи (Рис.3) можно завершить до полноценного тора, где длина цилиндрического проводника стремится к нулю.
Расчет МП тора приведен далее.

Список литературы.
1) И.Е. Тамм // "Основы теории электричества", М, Наука, главная редакция физико-математической литературы, 1989. с.504.
2) С. Г. Калашников // “Общий курс физики”, том 2, государственное издательство технико-теоретической литературы, Москва, 1956.
3) С. Ю. Таскаев // Физика плазмы, сентябрь, 1997, т.23, №12, с.1123; “Динамика потенциалов при нагреве струи в пробкотроне атомарными пучками”.
4) Т. С. Симонен // Физика плазмы, сентябрь, 1997, т.23, №9, с.771; “Устойчивость плазмы с высоким давлением при благоприятной кривизне силовых линий магнитного поля”.
5) С. В. Путвинский// УФН, ноябрь 1998, т.168, №11, с.1235; “Возможна ли будущая мировая энергетическая система без ядерного синтеза”.
6) “Физический энциклопедический словарь”, гл. редактор А. М. Прохоров, Москва, “Советская энциклопедия”, 1983.
